Martingales and Pólya’s Urn
Published:
Consider an urn which begins with two balls, one white and one black. At each time $n = 1, 2, \dots$, a ball is chosen uniformly at random and duplicated in the urn. What happens in the long run?
This is an exercise in Williams’ Probability with Martingales, but I think it is instructive to see how martingales can be “found” naturally when you look for them, a lá the method of summation factors taught in Concrete Mathematics.
Let $B_n$ be the number of black balls chosen by time $n$, so that $B_0 = 0$ and $B_1$ is uniformly distributed on ${0, 1}$. The proportion of balls that are black after time $n$ is
\[M_n = \frac{B_n + 1}{n + 2}.\]I have suggestively called this “$M_n$” for “Martingale.” Indeed, $M_n$ is a martingale adapted to the sequence of sigma algebras defined by $F_n = \sigma(A_1, \dots, A_n)$, where $A_n = [\text{a black ball was chosen at time $n$}]$. It is not hard to check that this is true, but it seems lucky to me that exactly what we want to study happens to be a martingale. What if we were not so lucky? What if we had to define a martingale from scratch?
Let’s look for some motivation from our current problem. To check that $M_n$ is a martingale, we will need to compute $E_n[B_{n + 1}] = E[B_{n + 1} | F_n]$, so we may as well do that now:
\[\begin{align*} E_n[B_{n + 1}] &= B_n + E_n[[\text{black at time $n$}]] \\ &= B_n + \frac{B_n + 1}{n + 1} \\ &= (1 + 1 / (n + 1)) B_n + \frac{1}{n + 1}. \end{align*}\]Okay, we now know that $E_n[B_{n + 1}]$ is related to $B_n$ by some type of equation. Can we see how to define a martingale from here? Yes!
In general, suppose that the sequence of random variables $B_n$ satisfies
\[E_n[B_{n + 1}] = a_n B_n + b_n\]for some constant sequences $a_n$ and $b_n$. Let’s try to make a martingale by defining $M_n = c_n B_n + d_n$ for some to-be-determined constant sequences $c_n$ and $d_n$. To make $M_n$ a martingale, we need
\[E_n[M_{n + 1}] = c_{n + 1} (a_n B_n + b_n) + d_{n + 1} = c_n B_n + d_n = M_n.\]It would suffice to choose $c_n$ such that
\[c_{n + 1} a_n = c_n\]and $d_n$ such that
\[c_{n + 1} b_n + d_{n + 1} = d_n.\]But these conditions are easy to satisfy! They give, say,
\[c_{n + 1} = c_1 \prod_{k = 1}^n a_k^{-1}\]and
\[d_{n + 1} = d_1 - \sum_{k = 1}^n c_{k + 1} b_k.\]In the case of our exercise, we have $a_n = 1 + 1 / (n + 1)$ and $b_n = 1 / (n + 1)$. If we solve the implied recurrences (being thankful that the sum which occurs in $d_{n + 1}$ telescopes), then we get precisely
\[c_n = d_n = \frac{1}{n + 2},\]so the $M_n$ we would define is
\[M_n = \frac{1}{n + 2} B_n + \frac{1}{n + 2} = \frac{B_n + 1}{n + 2}.\]Magic!
Now that we have this martingale, what does it get us? Well, immediately it tells us that
\[E[M_n] = E[M_0] = \frac{1}{2},\]so we should always “expect” there to be a pretty even mix of balls in the urn.
What else? Well, this is a nonnegative (bounded!) martingale, so it has a limit almost surely. Call that limit $M_\infty = \lim M_n$. What does this limit look like?
Let’s take a moment generating function approach. Perhaps we can work out $E[\exp(M_n z)]$, and then take a limit to get $E[\exp(M_\infty z)]$.
Exercise: If $B_n$ is as defined before (the number of black balls chosen by time $n$), then $B_n$ is uniformly distributed on ${1, 2, \dots, n + 1}$. (Hint: Work out a recurrence using the law of total probability.)
Using the above exercise, we can write
\[E[\exp(M_n z)] = \sum_{k = 1}^{n + 1} \exp\left( \frac{(k + 1) z}{n + 2} \right) \frac{1}{n + 1}.\]This is just a geometric sum, a task fit for a computer. Maple readily spits out
\[E[\exp(M_n z)] = \frac{1}{n + 1} \frac{e^{(n + 4) z / (n + 2)} - e^{2z / (n + 2)}}{e^{z / (n + 2)} - 1}.\]Maple can also take the limit for us (but it is not so hard by hand in this case) to show that
\[\lim_n E[\exp(M_n z)] = \frac{e^z - 1}{z}.\]Well! This is intensely interesting. The function on the right is the moment generating function for the uniform distribution on $(0, 1)$! Could this be true? Could the limit of a discrete process be a continuous one? Look at these graphs:
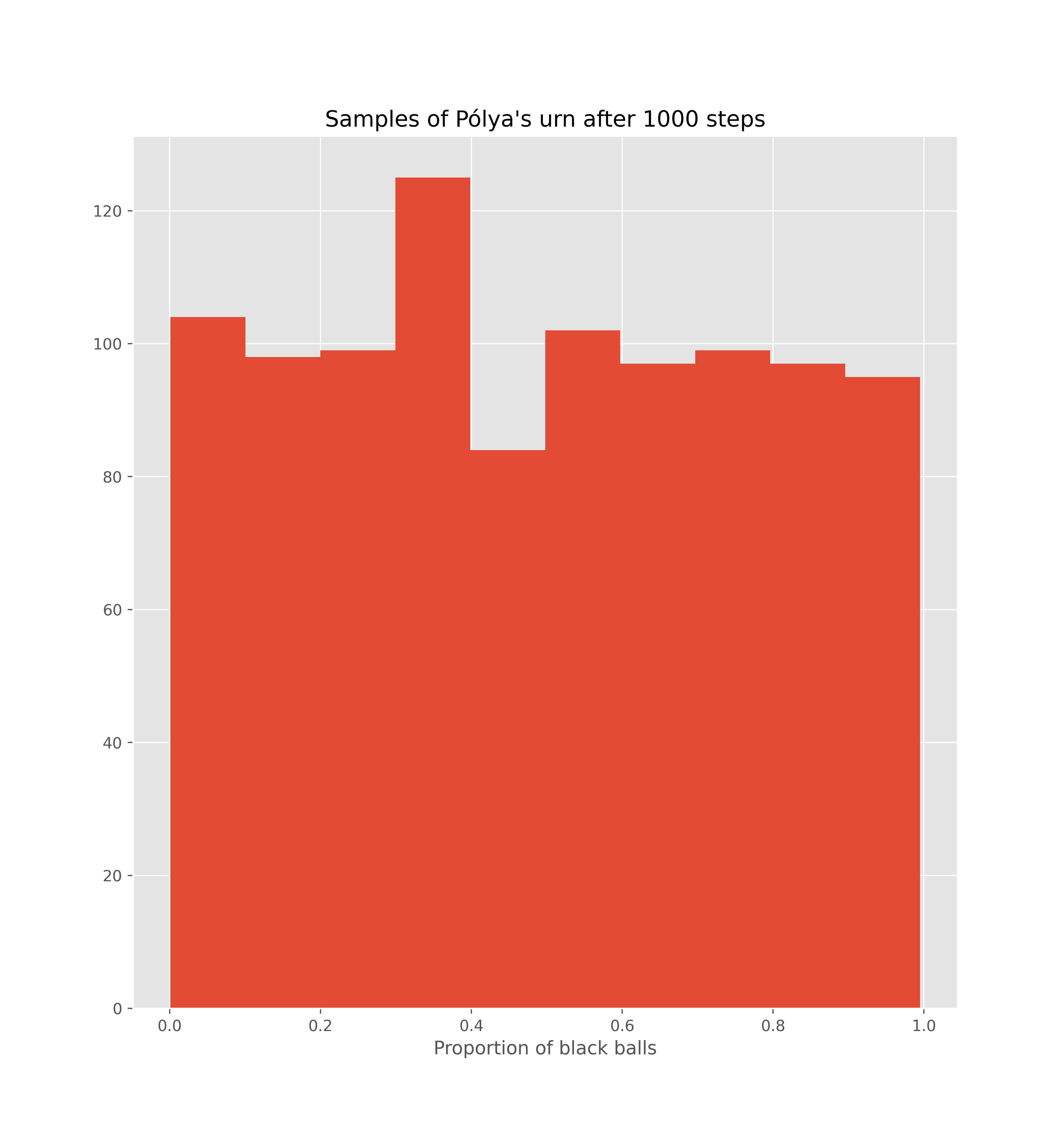
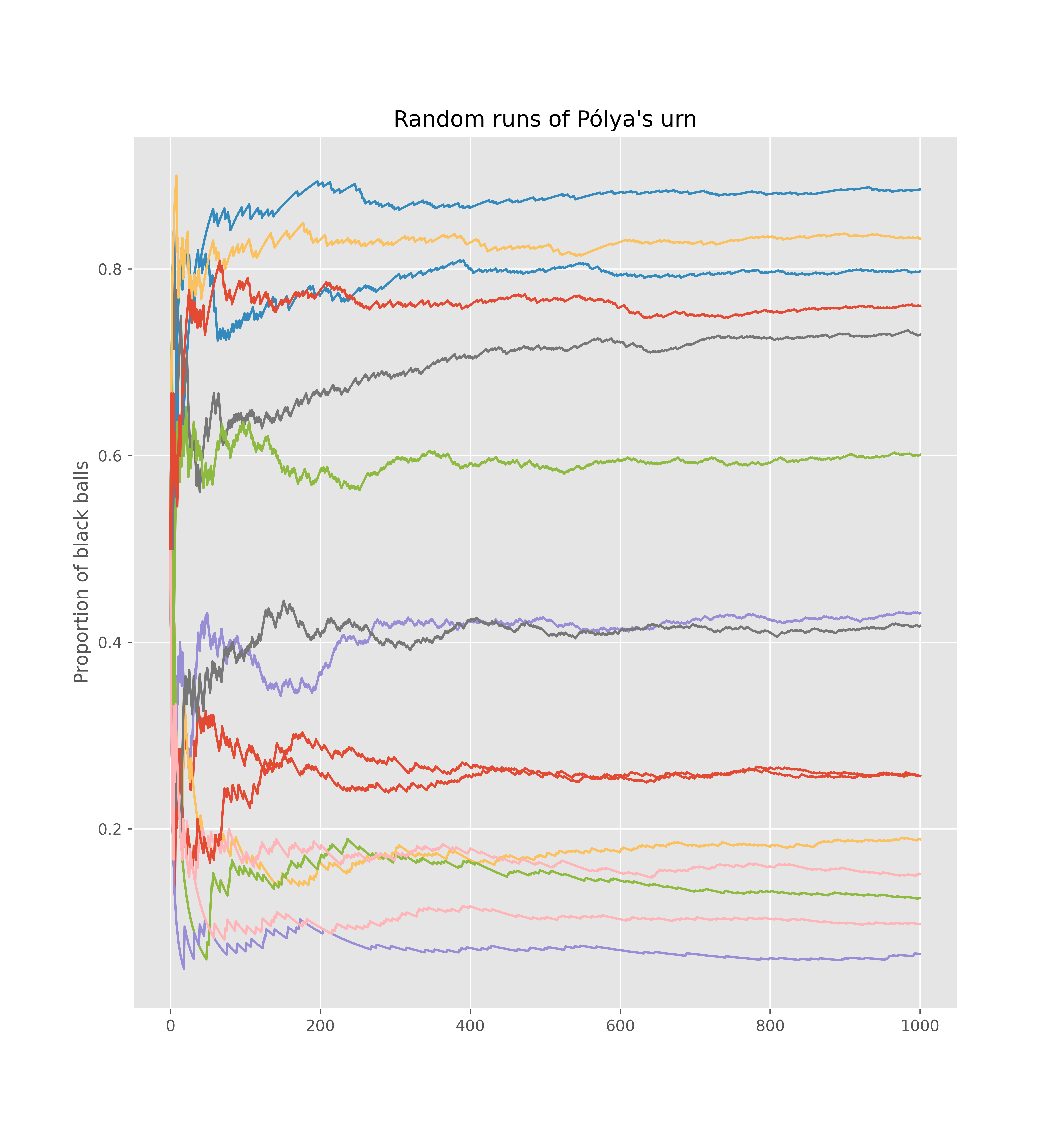
Why, it must be true! The graphs confirm it!
To assuage the hardened hearts of doubters, we should justify that
\[\lim_n E[\exp(M_n z)] = E[\exp(M_\infty z)].\]This is not hard:
\[|\exp(M_n z)| = \exp(M_n \operatorname{Re} z) \leq e\]for $|z| < 1$, say. So we can apply the dominated convergence theorem to get our moment generating function
\[E[\exp(M_\infty z)] = \frac{e^z - 1}{z},\]which shows once and for all that $M_\infty$ is in fact uniform on $(0, 1)$. Wow!
I’ve been thinking a lot about martingales for a probability class I’m taking this semester. I still don’t quite get them, but I’m trying to do more and more exercises to understand why we care about them. I have seen some good examples so far, but I’m just now getting to writing down some of my favorites.