The math department at Rutgers hosts weekly experimental mathematics seminars dedicated to results or techniques which have some “experimental” flair. A few months ago, OEIS-founder Neil Sloane showed me a fascinating sequence (A326344) before the seminar:

This sequence is generated by the following rule:

• $a(1) = 1$.
• If $n$ is prime, then $a(n + 1)$ is the next prime after $a(n)$, with its digits reversed.
• If $n$ is composite, then $a(n + 1)$ is the next composite after $a(n)$, with its digits reversed.

For example: To compute $a(2)$, note that 2 is prime, and find the next prime after $a(1) = 1$, which is 2 itself. We reverse the single digit of 2, and we get 2 again, so $a(2) = 2$. The sequence is boring until $a(10)$: $10$ is composite, so we ask for the next composite after $9$ and get $10$, which yields $1$ when reversed. Things get more interesting at $a(17)$: $17$ is prime, and the next prime after $a(16) = 9$ is 11, which reversed is 11. This is the first term with two digits.

This strange sequence has a surprising property, which we can observe by looking at its graph:

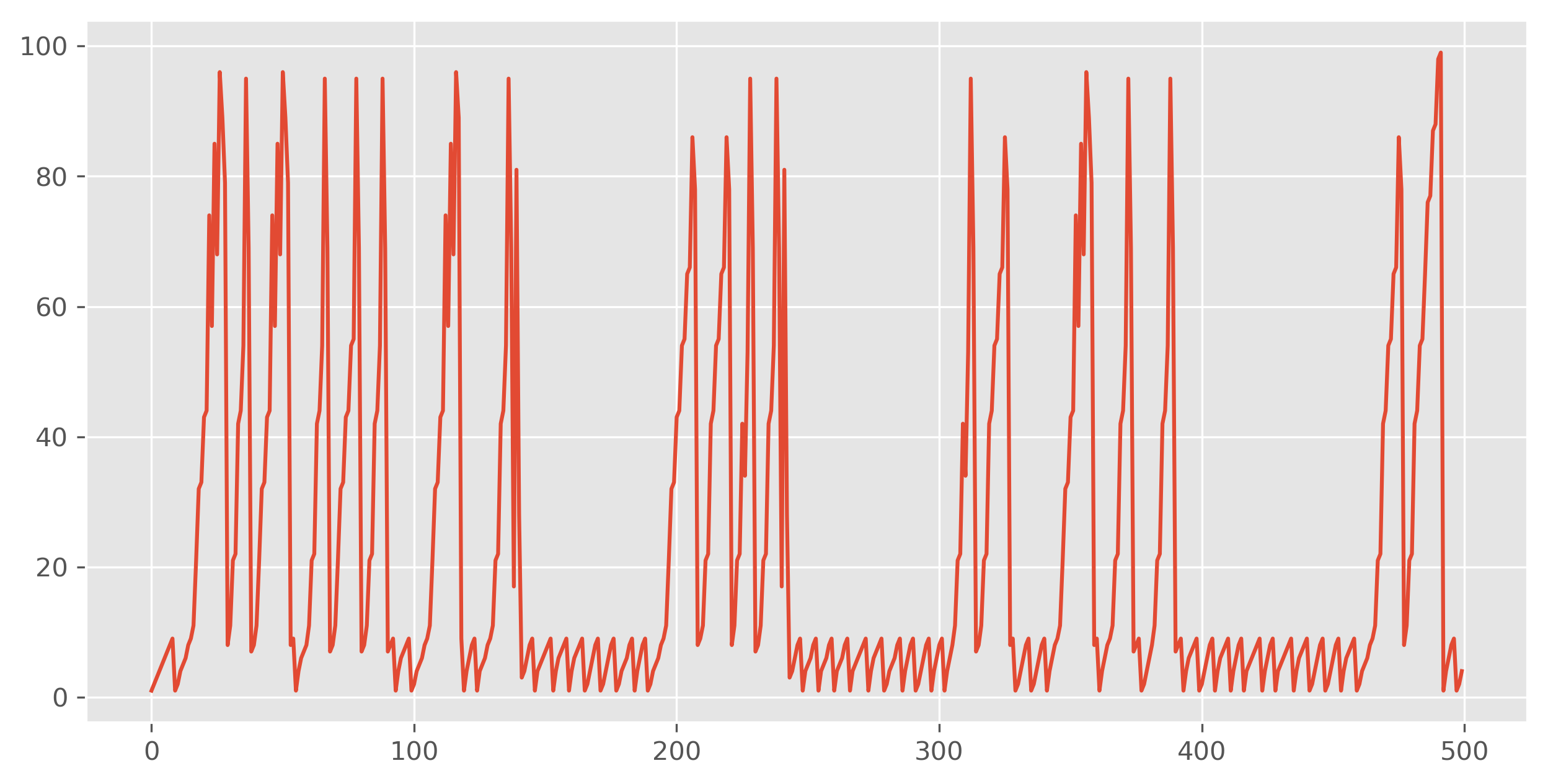
The sequence looks bounded! I’ve only shown the first 500 terms or so, but this pattern persists for hundreds of thousands of terms. In fact, the pattern persists forever: $a(n) \leq 909$ for all $n$, and this upper bound is achieved.

This is spooky. Why should the sequence be bounded at all? Why 909? How can you prove anything about such a weird sequence? This is what we’ll talk about here.

First, before continuing, I have code to play with this sequence:

• Raw Python
• Jupyter Notebook
• View Jupyter Notebook online

Proving the bound

When our sequence was first submitted, Michel Marcus reported that 909 was the maximum value up to $10^8$ terms. This is hard to prove because the sequence is highly irregular. Sometimes you apply the composite rule; sometimes you apply the prime rule. An induction argument has very little power in its inductive hypothesis because it can’t discern which rule should apply, or what rule was last applied. The picture looks something like this:

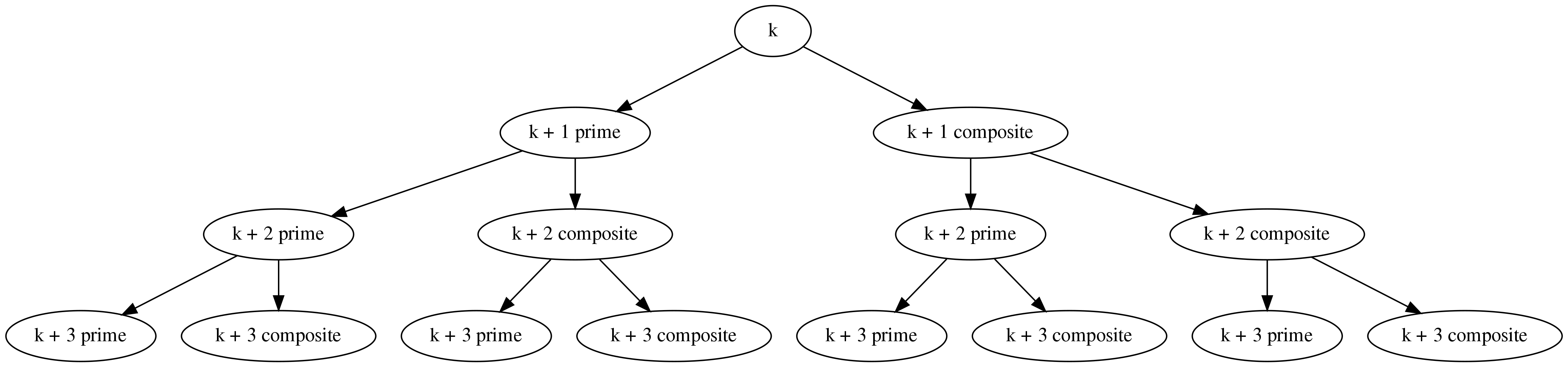
We need to reduce the number of possible branches to make sense of anything here. One way to do this is with a “modulus” argument. Essentially, it is easier to think about our sequence in blocks of residue classes with some nice modulus, like 2, 6, or 30. This way, you know which terms in the block are definitely composite, which are possibly prime, and so on.

For example, suppose that we try to prove something about our sequence by inducting on blocks of two consecutive terms. One of these terms has even index, so the composite rule applies. The other has odd index, so potentially either rule applies. There is still some branching, but now half as much:

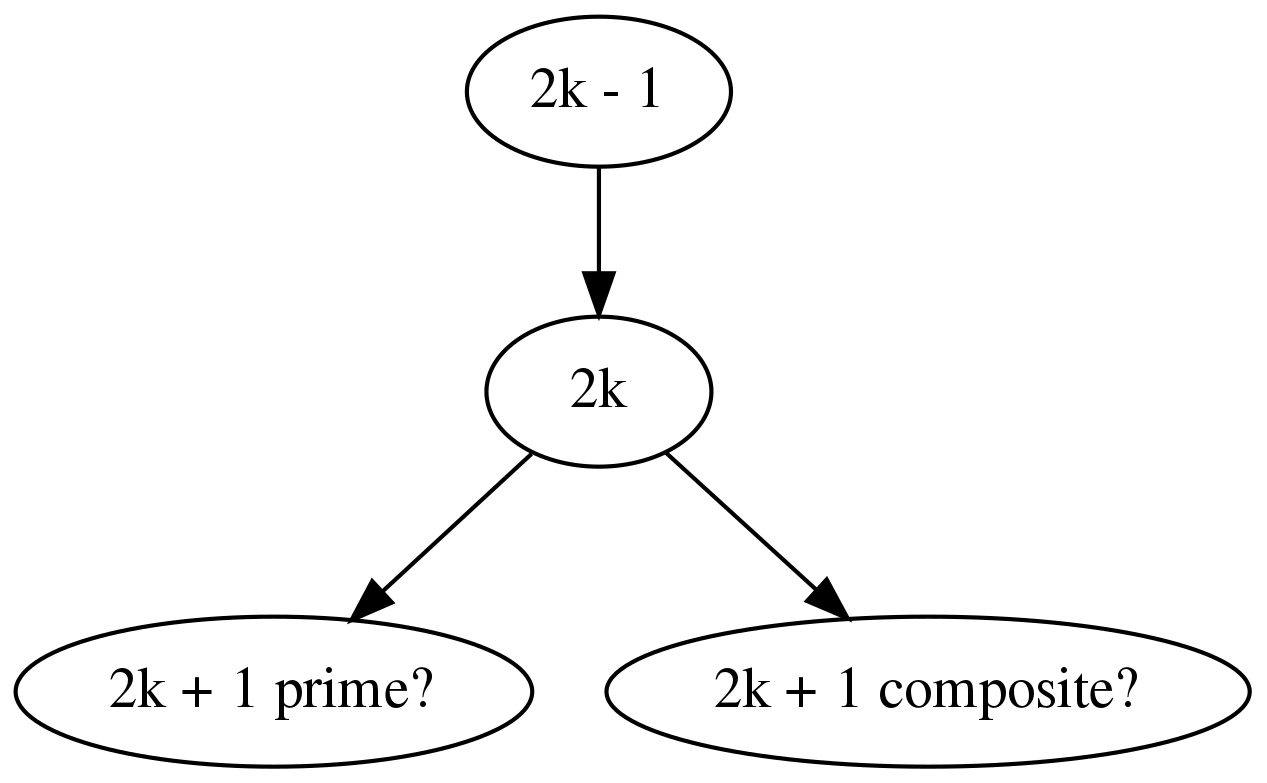
This is the modulus argument where we use 2 as our modulus. If we chose a different modulus, say 6, then we can cut down on the branching even further:

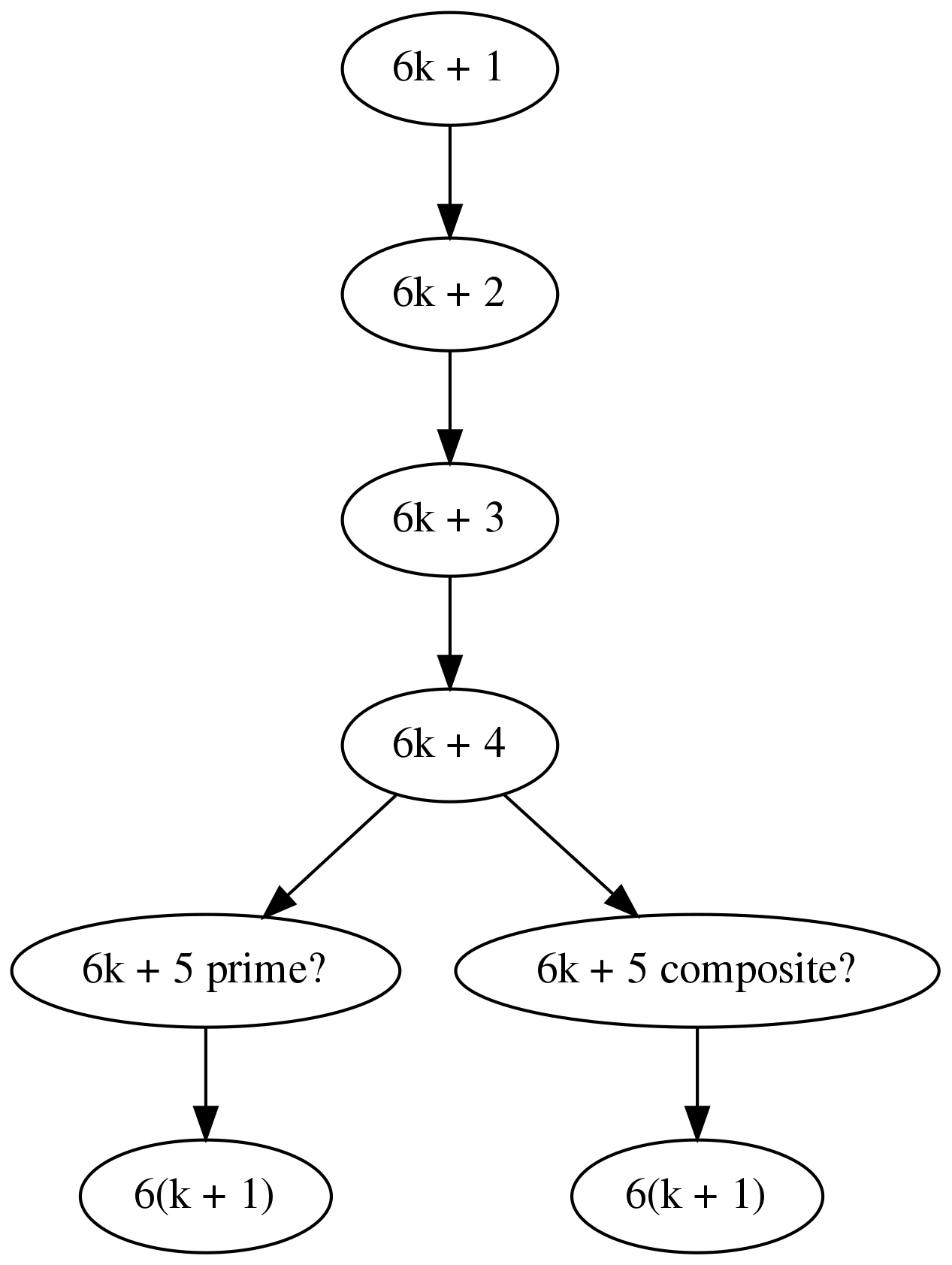
“Larger” moduli will rule out more residue classes as composite¹. We can use this idea to construct computational proofs that our sequence is bounded.

In fact, the argument proceeds almost exactly how I’ve drawn it here. We will construct a tree which contains all possible values of our sequence (possibly more than needed). The nodes of our tree will be labeled with $(r, x)$ pairs, where $r$ is the residue class in our modulus and $x$ is the possible value of the sequence.

The procedure goes like this: Choose a modulus $m$ and compute the first $m$ terms of the sequence². Let $x_0 = a(m + 1)$, and begin with a root note labeled $(1, x_0)$. Iteratively do the following:

• Visit a new, unseen node $(r, x)$.

• If the residue class $r$ mod $m$ forces the index to be composite, then add a descendent of $(r, x)$ using the composite rule.

• If the residue class $r$ mod $m$ allows the index to be prime, then add two descendants of $(r, x)$: one using the composite rule and one using the prime rule.

• Mark any added descendants as new nodes to visit if we haven’t already seen them.

• Add $(r, x)$ to a list of “seen” nodes.

• Repeat until there are no unseen nodes.

If this process terminates, then you have constructed a tree which (with the first $m$ terms) contains all possible values of the sequence $a(n)$. The maximum value of $x$ for all pairs $(r, x)$ will be an upper bound of $a(n)$.

Code to produce this tree looks something like this:

def generate_tree(residue, value, modulus):
    """
    :residue: Starting residue class.
    :value: Starting value of the sequence.
    :b: Base of the sequence.
    :modulus: Modulus for the modulus argument.
    """

    possible_prime_vals = find_possible_prime_vals(modulus)

    # Contains (n mod modulus, value) pairs.
    seen = set()
    # Contains (n mod, value) pairs.
    to_visit = [(residue % modulus, value)]

    while to_visit:
        mod, term = to_visit.pop()

        if (mod, term) in seen:
            continue

        seen.update({(mod, term)})
        next_mod = (mod + 1) % modulus

        next_comp = backwards(nextcompo(term))
        if (next_mod, next_comp) not in seen:
            to_visit.append((next_mod, next_comp))

        if next_mod in possible_prime_vals:
            next_prime = backwards(nextprime(term))
            if (next_mod, next_prime) not in seen:
                to_visit.append((next_mod, next_prime))

    return seen

If we carry out this procedure with a modulus of $6 = 2 \cdot 3$, then we obtain a tree with maximum observed value $909$. Therefore $a(n) \leq 909$.

These arguments have little to do with our sequence itself. The same idea would apply to any sequence which depends on a rule that can be affected by knowing the residue class of an index.

The original arguments

Rémy Sigrist gave the first proof of any bound, essentially using the modulus argument with 2.

Sigrist’s argument is computational: Create a set EVEN for the values of $a(n)$ which occur at even values of $n$. If, say, $a(2n)$ is an element of EVEN, then there are two possible “next” values for $a(2n + 1)$, corresponding to the two different rules we could apply from our sequence. After we know those two values, the next possible $a(2n + 2)$ can be computed using the composite rule.

More explicitly, let $p$ be the “next prime and reverse” function, and $c$ be the “next composite and reverse” function. If $x$ is in EVEN, then so is $c(p(x))$ and $c(c(x))$, and these are all the possible elements we could ever obtain at even indices.

Every value of $a(2n + 1)$ is the result of applying one of $p$ or $c$ to an even value, so the corresponding set ODD is contained in the image of EVEN under $p$ and $c$. If our process terminates, then we have a finite set which contains the image of $a(n)$, which gives us some upper bound. This upper bound may be larger than strictly necessary, but it would be better than nothing.

This method gives us $a(n) \leq 939$.

Here is a short function to automate and illustrate this argument:

def generate_terms(a0, p, c):
    """
    Compute a containing set for the terms of a sequence a(n)
    where a(n) = c(a(n - 1)) if n is even, and a(n) is in
    {p(a(n - 1)), c(a(n - 1))} if n is odd.
    """
    terms = {a0}

    while True:
        new_terms = (terms
                      | set(map(c, map(p, terms)))
                      | set(map(c, map(c, terms))))

        if new_terms != terms:
            terms = new_terms
        else:
            break
    even_terms = terms
    odd_terms = set(map(p, even_terms)) | set(map(c, even_terms))
    return even_terms, odd_terms

This method is essentially identical to the general modulus argument with 2 as the modulus. It avoids explicitly mentioning the tree by keeping values in the EVEN and ODD sets.

Andrew Weimholt obtained the correct bound of 909 by using a modified form of the modulus argument with modulus 6. His modification consists of starting the trees from values where $a(n)$ could “escape” single digits, then terminating a branch if it ever returns to single digits. His algorithm is therefore something like this:

1. Determine all values of $a(n)$ where $a(n)$ could possibly “escape” single digits. Here, this can only occur if $a(n) = 11$. Further determine what the possible classes mod 6 are possible for such $n$.

   (This really can be done explicitly. If $a(n) < 10$, then the only way to exceed $9$ is to ask for the next prime when $a(n) = 9$. This means that $11$ is the only possible “escape” value, and it had to occur when $n \bmod 6$ was $1$ or $5$, otherwise $n$ would be composite.)

2. For each possible escape value and corresponding class mod 6, construct a tree of possible values of $a(n)$ after this escape value. Each level of the tree is a different residue class mod 6, and descendants are the possible next values of the sequence. Terminate a branch if it ever reaches single digits again (or something else you’re tracking).

If the trees constructed in step 2 are finite, then all values of $a(n)$ which are greater than 9 must exist in them. Computing the maximum elements in each tree will give us another upper bound for $a(n)$.

Here is an example of two such trees, produced by Weimholt himself³:

n mod 6
-----------------------------------------
   1      11
   2      21      
   3      22
   4      42_______________________
   5*     44                     34
   0      54___________          53______
   1*     55         95          45    95
   2      65         69          64    69    
   3      66         [7]         56    [7]
   4      86______               75___________
   5*     78    98               67         97
   0      [8]   99__________     86______   89______
   1*           [1]    [101]     78    98   [9]   79
   2                             [8]   99         [8]
   3                                   [1]

n mod 6
-----------------------------------------
   1      101
   2      201
   3      202
   4      302_______________
   5*     303            703
   0      403_______     407_______
   1*     404    904     804    904
   2      504    509     508    509
   3      505    [15]    [15]   [15]
   4      605_______________
   5*     606            706
   0      806_______     707_______
   1*     708    908     807    907
   2      [17]   909     808    809
   3             [19]    [18]   [18]

Weimholt’s tree argument also gives us the right bound: $a(n) \leq 909$.

This ends the story of A326344, but there is certainly more.

In alternate bases

In the definition of A326344, we mentioned reversing the digits of numbers. Implicitly, we meant the decimal, i.e., base 10 digits. Had we specified another base, we would have gotten another sequence. (In base 10, reversing 11 gives 11. In base 5, we have 11 = 21_5, so reversing the digits gives 12_5 = 7. This really is new!) To this end, define a new family of sequences $a_b(n)$ for each integer $b \geq 2$:

• $a_b(1) = 1$.

• If $n$ is prime, then $a_b(n + 1)$ is the next prime after $a_b(n)$, with its base $b$ digits reversed.

• If $n$ is composite, then $a_b(n + 1)$ is the next composite after $a_b(n)$, with its base $b$ digits reversed.

For example, $a_7(n)$ begins like this (in decimal):

The obvious question about $a_b(n)$ is whether it is bounded for all $b$. answer, so far, is probably. The modulus argument, when automated, seems to always succeed in tightly bounding $a_b(n)$ from above. The known maxima are given in A327701. However, we do not know if all of these sequences are bounded. I have some wonderful data to suggest that they are:

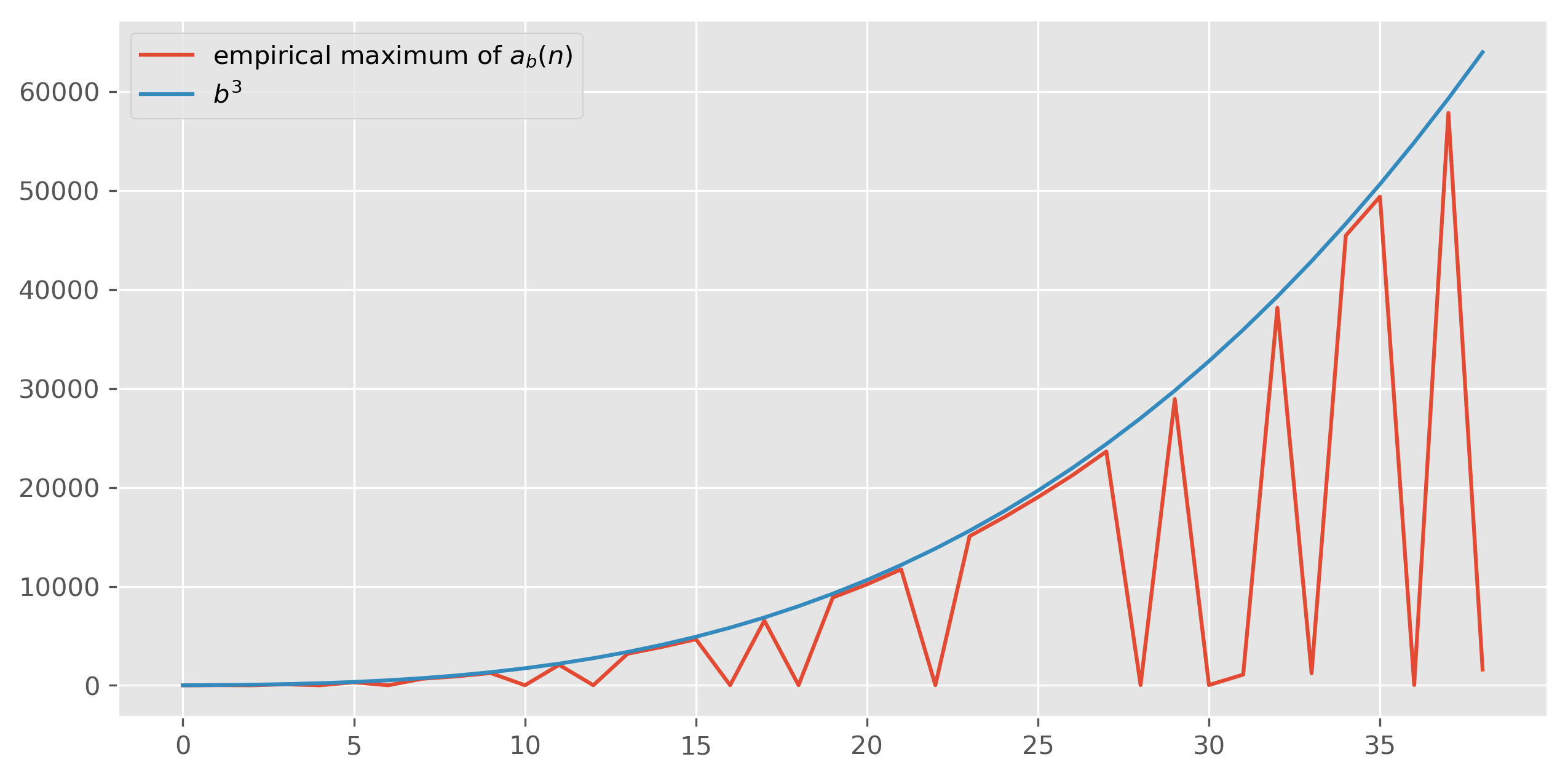
It seems like $a_b(n)$ is bounded almost perfectly by $b^3$. Thus far, I’ve had little success proving this. The modulus argument seems to always work, but it really depends on the particulars of each base. That is, it seems like each $a_b(n)$ gets “lucky” in how it remains bounded by $b^3$. It is mysterious why the modulus argument should always work. It is also mysterious why $b^3$ is the important quantity. Why not $b^2$? Or $b$? Or $b^{3 / 2}$?

For the time being, nearly everything about these sequences remains open.

Conjectures to prove

Here are a few conjectures about our family of sequences that would be nice to prove:

• $a_b(n) < b^3$.
• $a_b(n) < p$, where $p$ is the largest prime less than $b^3$.
• $\max_n a_b(n) = b - 1$ iff $b - 1$ is 1 or an odd prime.
  • I can prove that $\max_n a_b(n) = b - 1$ if $b - 1$ is 1 or an odd prime, and I can prove that the sequence exceeds $b - 1$ if $b$ is prime and $b-1$ is composite. I cannot prove that the sequence exceeds $b-1$ if both $b$ and $b - 1$ are composite.