Birthday Dominoes
Published:
(This post is dedicated to the most important Pisces birthday I know: EK.)
Dominoes is a well-known game that no one actually knows how to play. A much more accessible game is tiling dominoes: I give you a grid, and you tell me if you can cover the whole thing with dominoes.
For example, look at this 2x2 grid:
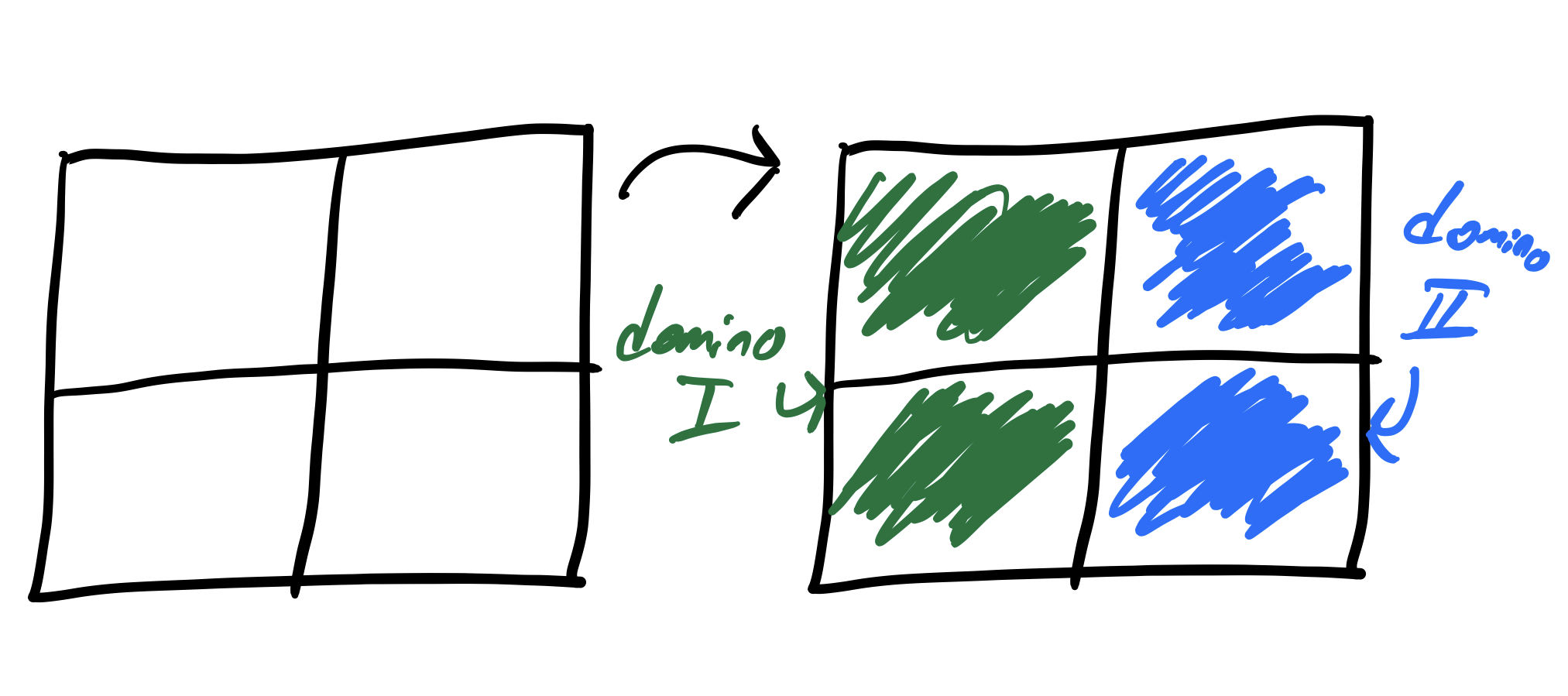
Easy! What about this 4x4 grid?
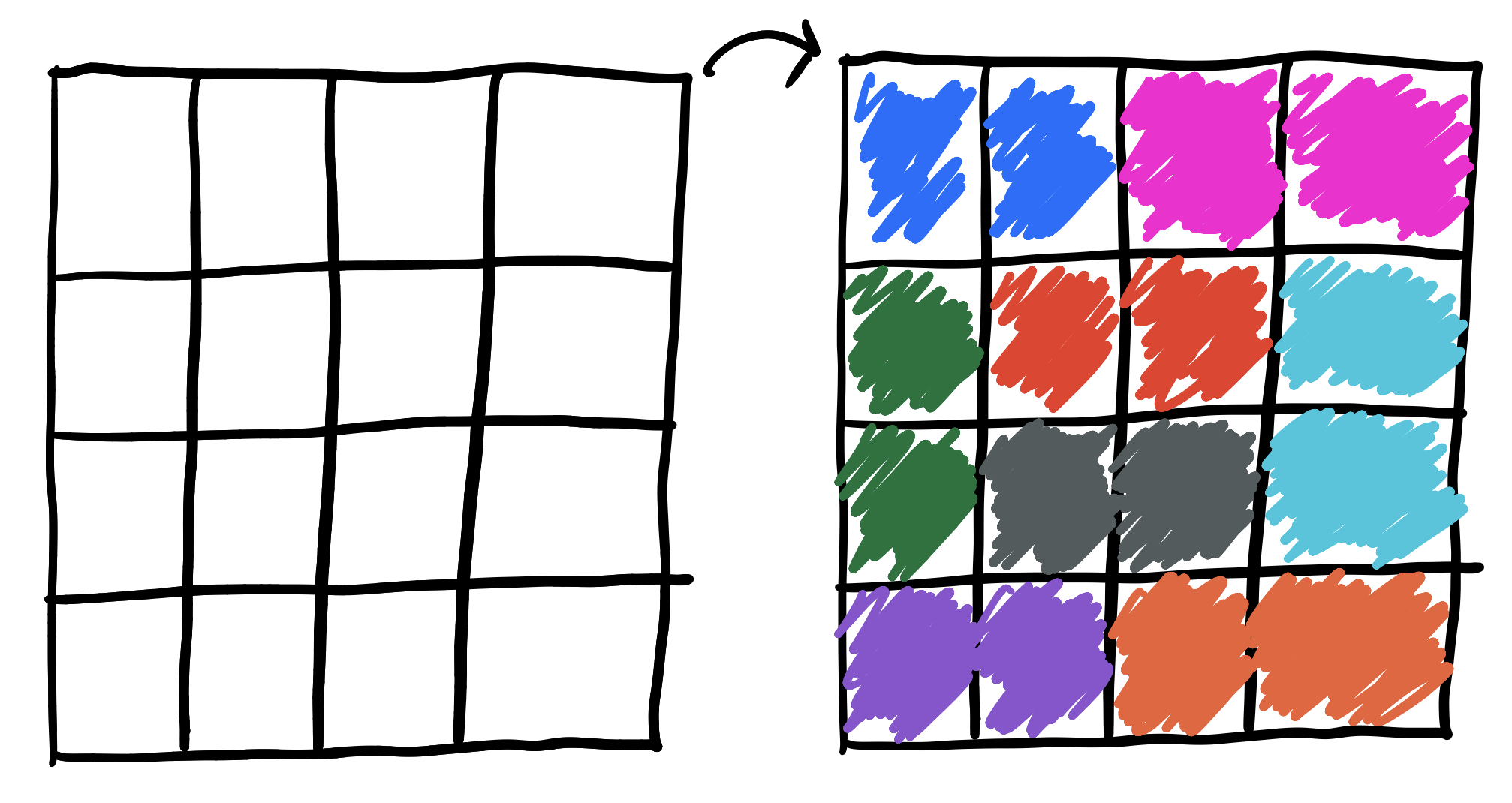
Also easy! What about a 3x3 grid?
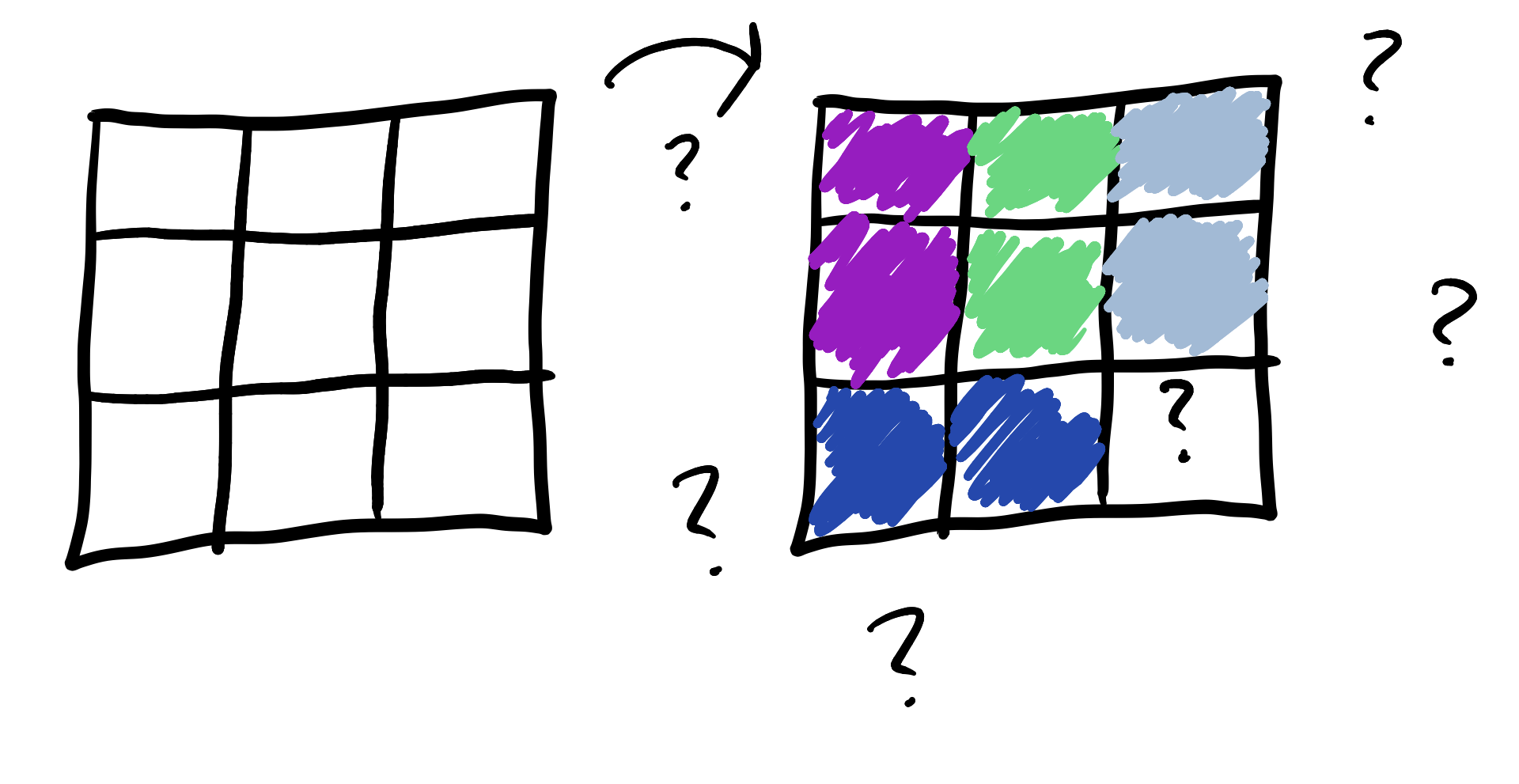
It can’t be done! Any grid you can cover with dominoes has to have an even number of squares, but a 3x3 grid has 9. We lose, through no fault of our own.
This pretty much solves grids. You can tile them with dominoes if and only if they have an even number of squares. But this gives us two natural questions to ask:
-
What if we used something other than dominoes?
-
What if we used something other than grids?
Something other than dominoes
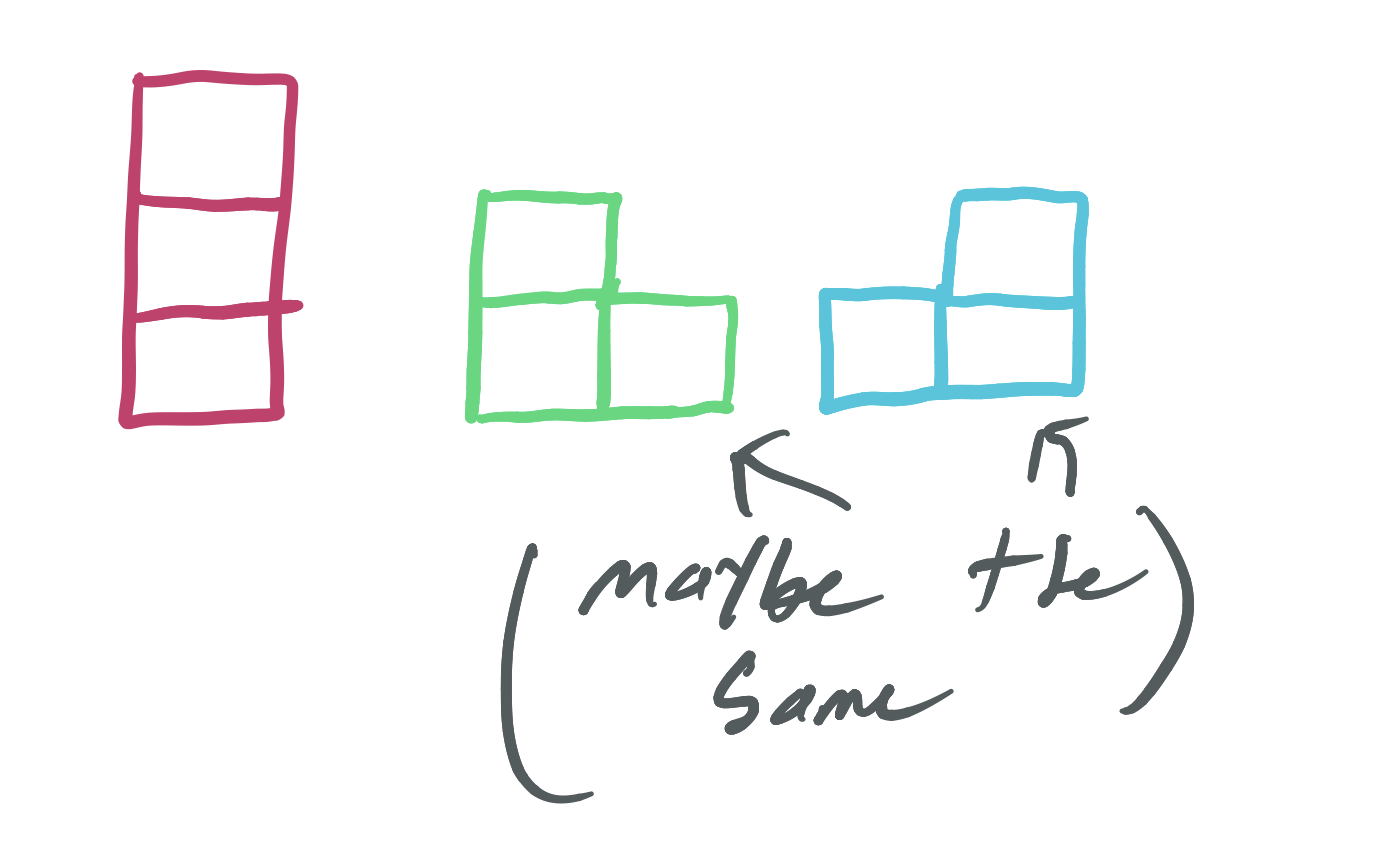
Dominoes are pieces with two blocks “snapped” together. What if we used more than two blocks? This these exist, of course, and we call them triominoes, quadominoes, pentominoes, and in general, polyominoes.
There is only “one” domino—two blocks stuck at their ends—but there are three triominoes!
That pesky 3x3 grid that we couldn’t tile with dominoes is a cinch with triominoes:
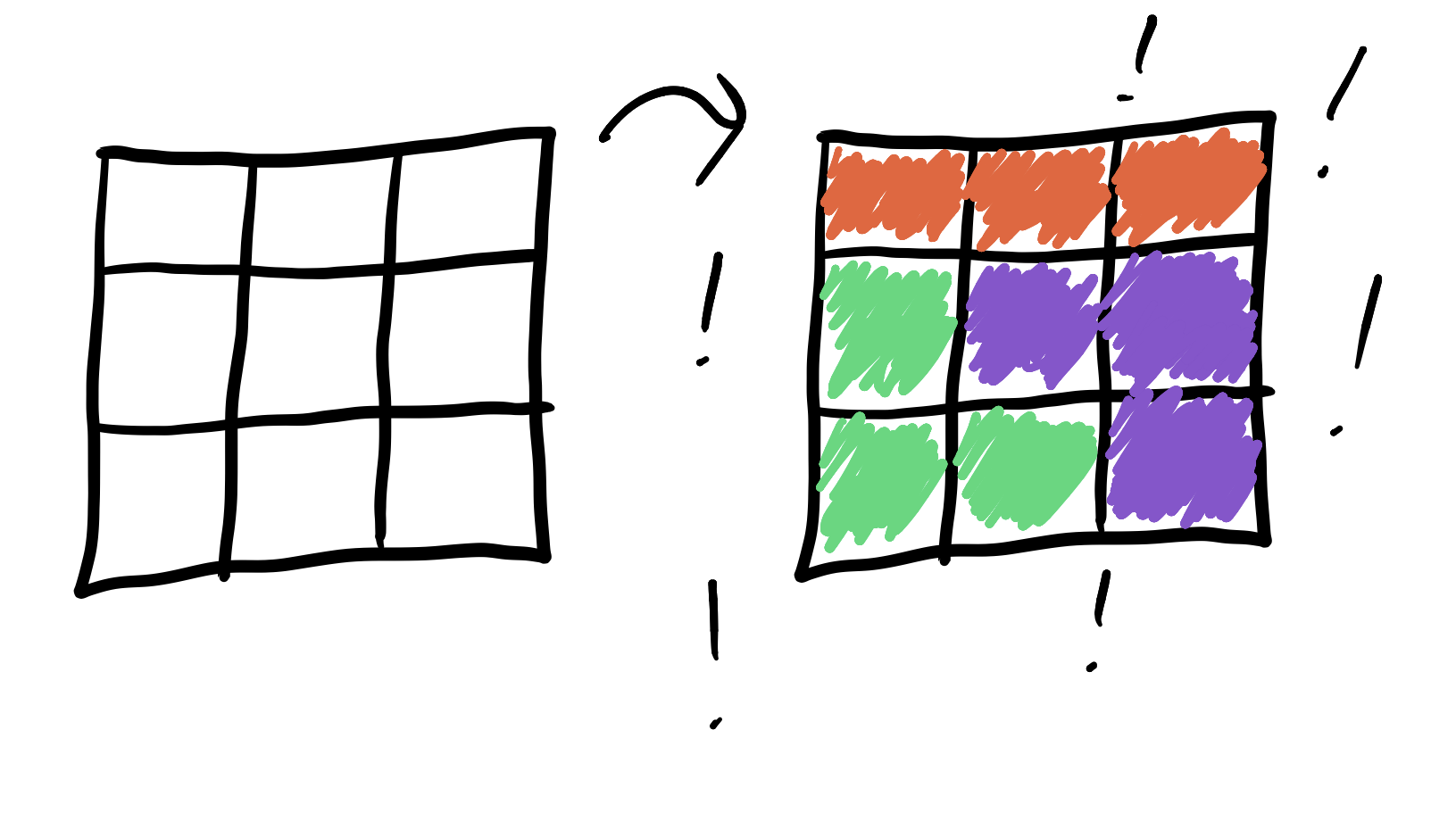
The most famous polyomino is the pentomino, which has five blocks stuck together. These are commonly used for fun in brain teasers, if you’re into that sort of thing.
Something other than grids
The shape of the board is just as important as the number of spaces. For example, look at this “T” with four spaces:
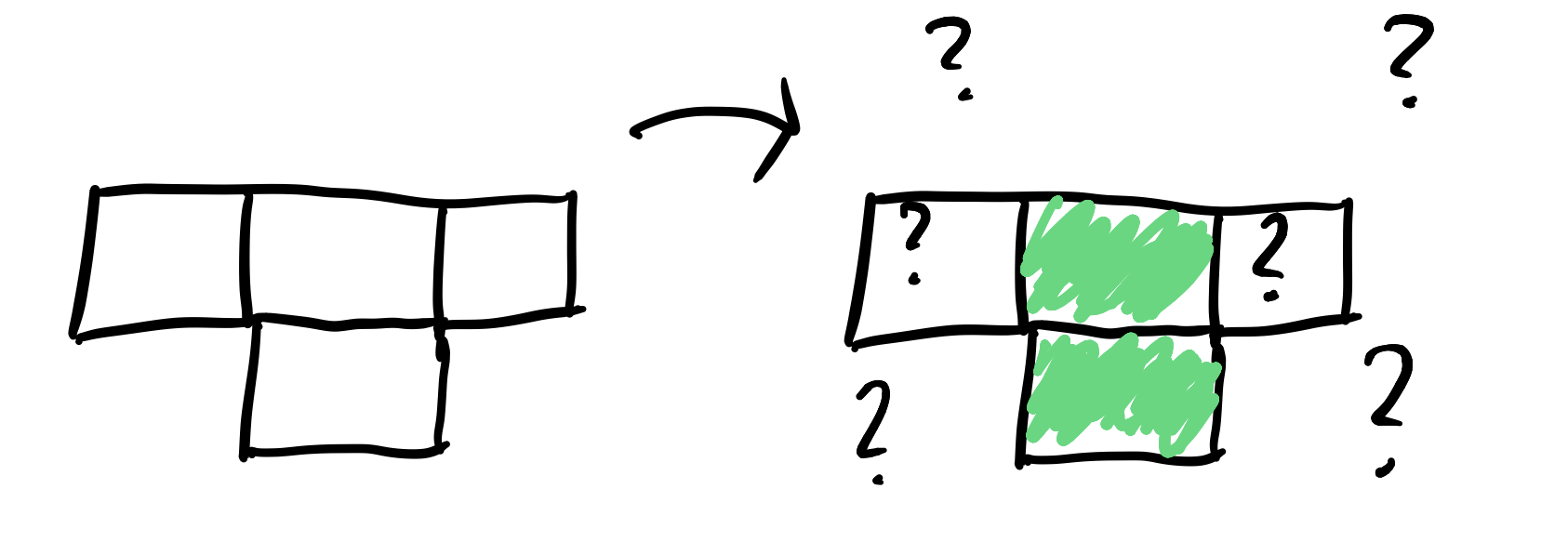
Even though there are an even number of spaces, we can’t tile this with dominoes! Here’s a grid with 9 spaces that we cannot tile with triominoes:
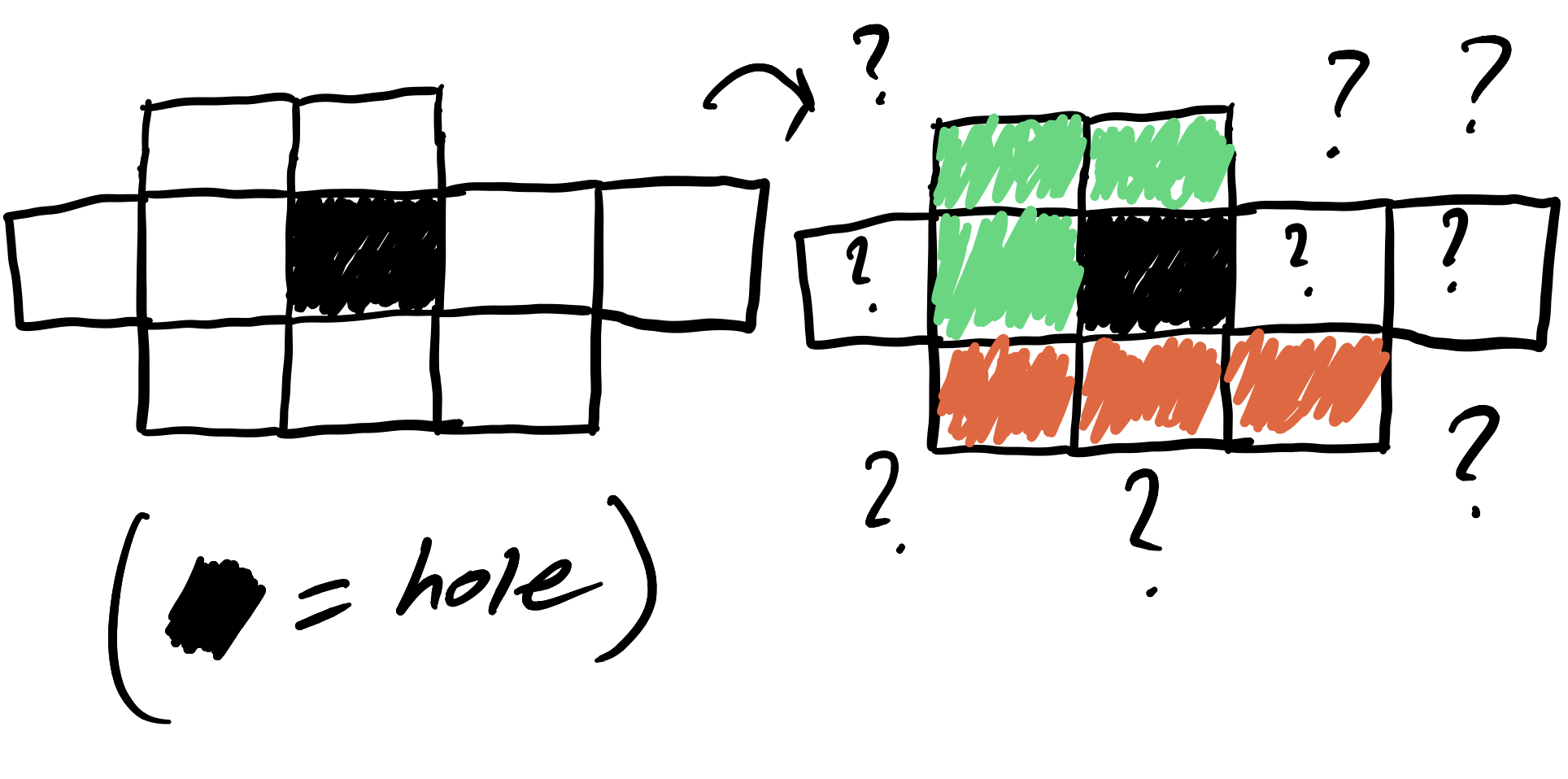
In general, a board with $n$ spaces is only guaranteed to have a tiling of monomioes (pieces with 1 block) and an $n$-omio (a piece with $n$ blocks), both of which are kind of cheating. Board layout plays a big role.
The heart board
I propose that we think about tiling the heart board, something I invented for just this occasion. Here are the first four heart boards:

It’s a bit hard to make out the “grid” in these pictures, so here are the first two drawn by hand (kinda):
The number of blocks in the first four hearts is 10, 43, 96, and 169, respectively. The hearts follow a pattern that generalizes to arbitrary sizes. The $n$th heart board is the set of all $(x, y)$ such that
- $0 \leq x < 2n$
- $0 \leq y < 4n$
- $x \leq y$
- $y \leq 5n - x$
- $y \leq x + 3n$,
and also the reflection of these points about the $y$-axis.
The $n$th heart board has exactly
\[10 n^2 + 3n - 3\]spaces in it.
There are lots of questions to ask about this board, but let’s settle for just one: When can the heart board be tiled by dominoes?
The first heart board cannot be tiled with dominoes. That’s easy enough to see by hand because it only has 10 blocks:
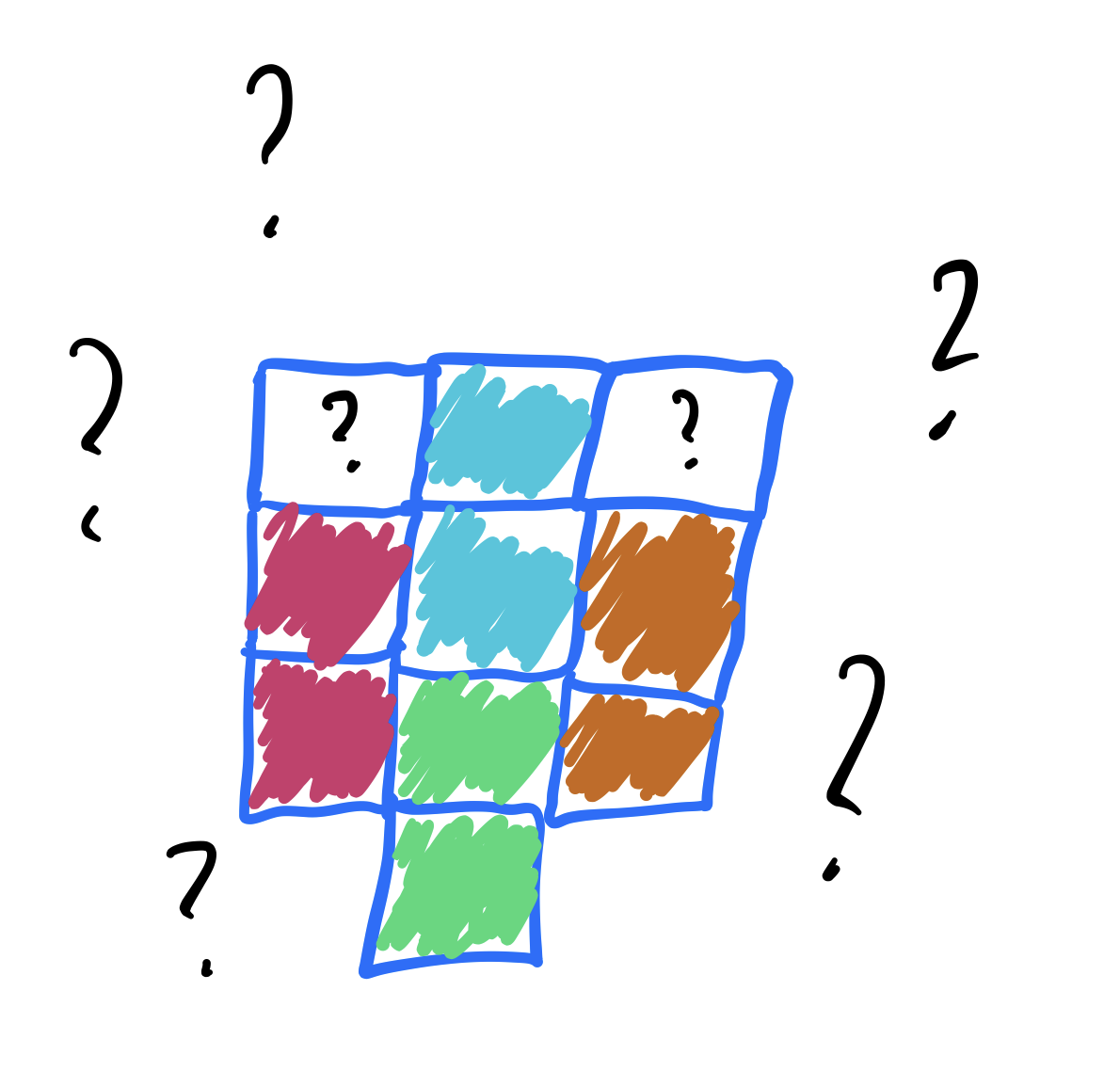
The second heart board is much bigger at 43 blocks, but this is an odd size so no tiling by dominoes could exist. In fact, the general size $10 n^2 + 3n - 3$ is odd when $n$ is even, so only the “odd” heart boards could hope to be tiled by dominoes anyway.
So what about the third heart block, the one in the bottom left of the computer-generated image above? Can it be tiled using dominoes? It turns out that no, it cannot be. How do I know this? My computer told me. In fact, using the polyomino library, my computer told me more:
| Heart board number | Domino tiling? |
|---|---|
| 1 | no |
| 3 | no |
| 5 | no |
| 7 | no |
| 9 | no |
| 11 | no |
| 13 | no |
| 15 | no |
| 17 | no |
| 19 | no |
It seems like no heart boards can be tiled by dominoes. Is this true? Amazingly, yes! Not a single heart board can be tiled by dominoes.
The proof of this fact relies on a very simple observation: If you color the squares of an odd heart board in an alternating fashion, then then there are exactly two more squares of one color than the other. For example, look at the first heart board:

Every domino you put down must cover exactly one of each color. In the above picture, every domino covers one red and one blue tile. Once you place four dominoes, there are no blue tiles left, but two red tiles. We can’t cover those pieces with dominoes! (This is what happened in our attempted tiling above.)
This pattern persists for every odd heart board. Here is a plot of the first four hearts again, now colored in this alternating way:

The first and third heart boards above (left column) have exactly two more red squares than blue squares. The second and fourth (right column) actually have a bigger difference in the number of squares, but we already knew that they couldn’t be colored with dominoes.
This pattern is somewhat tricky to prove, but once you know the idea it’s just calculations. See my math.SE question for details.
We’ve left lots of questions on the table that would be easy to answer. For example, what’s the proportion of squares that are red versus blue in the even heart boards? A harder project: Let $L_n$ be a set of lines which intersect the square $[-n, n] \times [0, n]$ and each other. When is the region “inside” $L_n$ tileable with dominoes?
I don’t know the answer to any of these offhand, but they sound fun. I hope that this delivery on my promise of math art taught everyone something new. Here’s to much more in the future!
